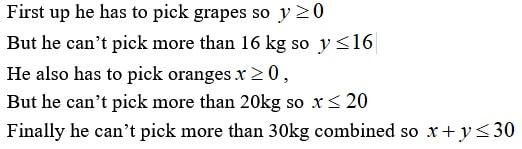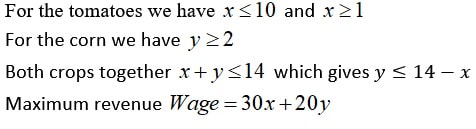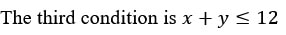Linear Programming
What you should know before you begin
Why Linear Programming?
Apart from the fact that it is compulsory now…Linear programming/optimization is a very applicable area of Mathematics where the student can see how Mathematics is used in real life and in decision making. It opens the door to an understanding in how businesses/corporations manage overheads, inventory and staff to gain maximum profits and to minimize costs.
The downside of this topic is that students need to be able to read as the questions can often be long
Each question consists of three main parts
1. Writing the inequalities
2. graphing the inequalities
3. identifying the feasible region and its vertices and using those vertices and the objective function to do the maximize or minimize as the case may be
- How to write inequalities from worded statements, how to solve them and represent the solution set on a number line
- How to plot and draw graphs of straight lines including simple linear transposition
Why Linear Programming?
Apart from the fact that it is compulsory now…Linear programming/optimization is a very applicable area of Mathematics where the student can see how Mathematics is used in real life and in decision making. It opens the door to an understanding in how businesses/corporations manage overheads, inventory and staff to gain maximum profits and to minimize costs.
The downside of this topic is that students need to be able to read as the questions can often be long
Each question consists of three main parts
1. Writing the inequalities
2. graphing the inequalities
3. identifying the feasible region and its vertices and using those vertices and the objective function to do the maximize or minimize as the case may be
|
|
The first two questions used in this section are taken from Living Mathematics Book 4 for Caribbean Examinations by P. Hill, page 215. This is the only textbook I have found that gives a complete treatment of the subject. If you can find a copy please give it a read.
|
Question 1
A boy finds he can pick no more than 20kg of oranges or no more than 16kg of grapes in a day. However he is told that he is not allowed to pick more than 30kg of fruit in total. If he is paid $3 for each kilogram of grapes and $5 for each kilogram of oranges, calculate how many kilograms of grapes and oranges he needs to pick to earn a maximum wage.
|
First thing we decide on the variables
Let x = the kg of oranges to be picked Let y = the kg of grapes to be picked Now we write the inequalities to represent the situation Note also that there is another function, his wage equation, sometimes called the objective function or profit function depending on the situation it is S = 5x + 3y. We do NOT graph this function |
The next step is to set up your graph paper and draw your graph. Note before drawing x+y<30, it has to be rewritten as y<30 - x and treated y = 30 -x. You don’t need more than two pairs of coordinates to draw a straight line graph. Note that for x = 0, y = 30 - 0 = 30 so one pair of coordinates is (0, 30). Also if x = 15, then y = 30 – 15 = 15, which gives another coordinate as (15, 15). Those two points are sufficient to draw this function
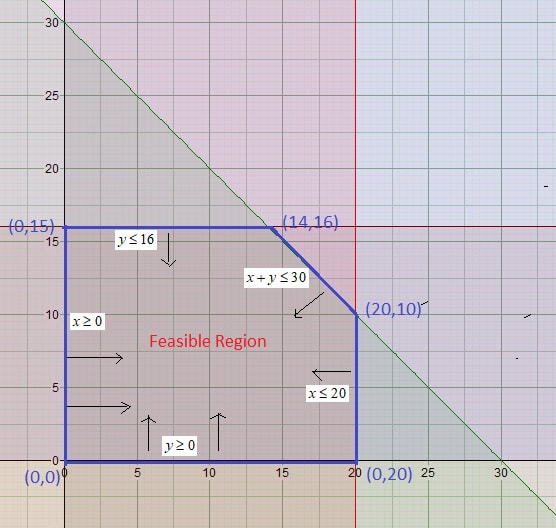
The graph below shows the inequalities plotted and the feasible region identified with the blue line
The graph below shows the inequalities plotted and the feasible region identified with the blue line
The feasible region by definition is the area where all your solutions reside. Every possible point in the space is a solution however the best solutions are located at the corner points.
So we look at those points (0, 0), (0, 20), (20, 10), (14, 16) and (0, 15). Each of these is substituted into the salary function to see which one gives the highest salary
Using (0, 0) we have Salary = 5(0) + 3(0) = $0
Using (0, 20) we have Salary = 5(0) + 3(20) = $60
Using (20,10) we have Salary = 5(20) + 3(10) = $130 [Maximum here]
Using (14,16) we have Salary = 5(14) + 3(16) = $118
Using (0, 15) we have Salary = 5(0) + 3(15) = $45
Using the results the decision that he should make is to pick 20kg of oranges and 10kg of grapes. That will give him the maximum salary of $130 per day
So we look at those points (0, 0), (0, 20), (20, 10), (14, 16) and (0, 15). Each of these is substituted into the salary function to see which one gives the highest salary
Using (0, 0) we have Salary = 5(0) + 3(0) = $0
Using (0, 20) we have Salary = 5(0) + 3(20) = $60
Using (20,10) we have Salary = 5(20) + 3(10) = $130 [Maximum here]
Using (14,16) we have Salary = 5(14) + 3(16) = $118
Using (0, 15) we have Salary = 5(0) + 3(15) = $45
Using the results the decision that he should make is to pick 20kg of oranges and 10kg of grapes. That will give him the maximum salary of $130 per day
Question 2
A gardener can plant no more than 10 rows of tomatoes in his garden but he wants to plant at least one row of tomatoes. His son would like to plant at least two rows of corn. Unfortunately the garden can only accommodate 14 rows of plants. When they sell the vegetables they will get $30 for each row of tomatoes and $20 for each row of corn. How many rows of each crop should they plant to get the maximum return for their produce?
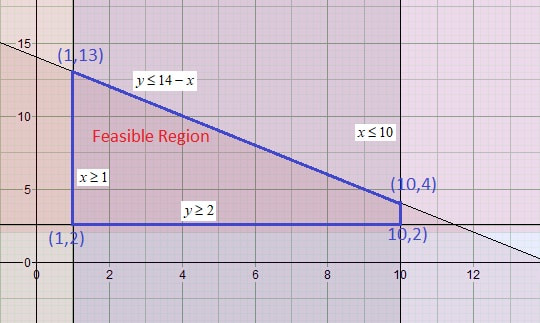
The graph of the inequalities is shown below
Using the corner points on the feasible region along with the objective function we get
Using (1, 2) we get a return of 30(1) + 20(2) = $70
Using (10, 2) we get a return of 30(10) + 20(2) = $340
Using (1, 13) we get a return of 30(1) + 20(13) = $290
Using (10, 4) we get a return of 30(10) + 20(4) = $380 [Maximum here]
To get the maximum return the gardener should plant 10 rows of tomatoes and his son should plant 4 rows of corn
Using (1, 2) we get a return of 30(1) + 20(2) = $70
Using (10, 2) we get a return of 30(10) + 20(2) = $340
Using (1, 13) we get a return of 30(1) + 20(13) = $290
Using (10, 4) we get a return of 30(10) + 20(4) = $380 [Maximum here]
To get the maximum return the gardener should plant 10 rows of tomatoes and his son should plant 4 rows of corn
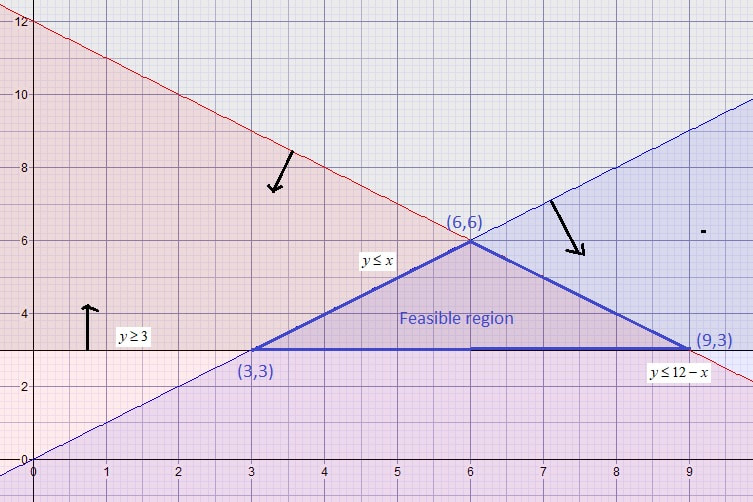
Question 3, May 2010 CXC #9b
The graph is shown below with the feasible region
Since we are looking for a minimum solution, the option of using 3 pumpkins and 3 melons is the best one
The file below contains practice questions from various CSEC papers, take a look and give them a try
| csec_linear_programing_questions.pdf | |
| File Size: | 1520 kb |
| File Type: | |